For most energy technologies, cost decreases with as the cumulative amount of deployment increases. Often, the cost is seen to decrease approximately the same amount with each doubling of the amount deployed. Straight line curve fits to cost data are commonly known as ‘learning curves’ and look like this:

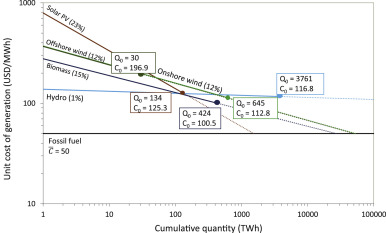Fig. 1. (from Shayegh et al., 2017) Learning curves for clean and conventional energy technologies. The horizontal axis represents cumulative quantity of electricity generation and the vertical axis represents the unit cost of electricity generation. Both scales are logarithmic. Learning rates (R) are shown in parentheses. Q0 indicates starting quantity and C0 is starting cost. With this axis scaling, straight lines represent power laws (Eq. (1)). We use data from this figure for subsequent analysis of the impact of different types of R&D (EIA, 2015, Wene, 2000 ; Rubin et al., 2015).

The idea is that as more of a technology gets deployed, people learn how to make the technology more cheaply, although economies of scale and other factors also play roles in bringing down costs.

I had the good fortune to be in a discussion with venture capitalists who were investing in companies doing research and development (R&D) on energy technologies. They mentioned that they didn’t want their R&D investment to just push them down the learning curve — they didn’t want to just learn things that they would have learned as production scaled up.

They said they want to shift the learning curve downward. They wanted to invest in innovations that would decrease cost as a result of innovations that would not come about simply by scaling up manufacture. (For example, maybe by shifting solar photovoltaic cells to a new kind of substrate.) This raises the question: If an R&D investment could reduce cost by the same amount by shifting the cost-starting-point of the learning curve downward (“curve-shifting R&D”) instead of effectively following the learning curve to that cost (“curve-following R&D”), which one would be better and how much better would it be?

---

To address this question, I got the help of Soheil Shayegh, a specialist in optimization and other mathematical and technical arts, and talked him into leading this project.

The “learning subsidy” is the total amount subsidy that would be needed to make a new more-expensive technology competitive with an incumbent technology. The needed subsidy to make a more expensive technology competitive in the marketplace starts out high but decreases as learning brings down the costs of the new technology (Fig 2a).

Figure 1 above shows cumulative quantity on the horizontal axis on a logarithmic scale, but such a figure can be redrawn with a linear axis, which turns the straight lines into curves. Figure 2 shows such curves for an idealized case:

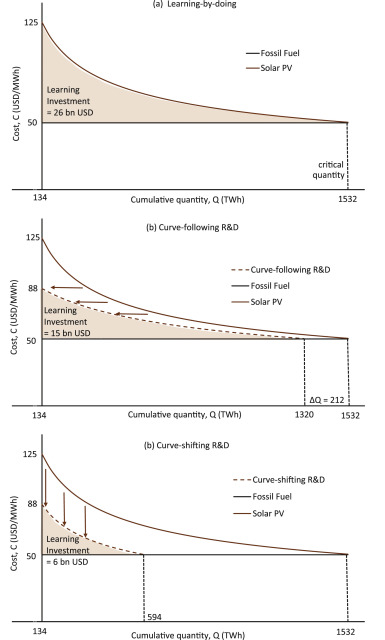
Fig. 2. (from Shayegh et al., 2017) Illustration of two stylized types of R&D for solar PV, a clean energy technology. (a) Learning-by-doing reduces the cost of the clean energy technology as the cumulative quantity of electricity generation increases. (b) Curve-following R&D reduces cost by producing the same knowledge as learning-by-doing, with an effect equivalent to increased cumulative quantity. (c) Curve-shifting R&D reduces cost by producing knowledge that would not have been gained by learning-by-doing, scaling the learning curve downward by a fixed percentage. The learning investment is the total subsidy necessary to reach cost parity with fossil fuels. For the same initial reduction in cost, curve-shifting R&D reduces the learning investment more than curve-following R&D. Note that horizontal and vertical scales are linear. The learning curves would be straight lines if both scales were logarithmic as in Fig. 1.

We found was that cost reductions brought about by breakthrough curve-shifting innovations were much more effective and bringing technologies closer to market competitiveness than were the same cost reductions brought about by incremental curve-following innovations. For example, that cost reductions in wind and bioenergy that come from curve-shifting research are more than 10 times more valuable than cost reductions that come about from curve-following research.

Further, we found in this idealized framework that the relative benefit of breakthrough innovations depended on only two things: (1) the initial cost of the new technology relative to the incumbent technology, and (2) the slope of the learning curve. The more expensive the new technology and the shallower the learning curve, the higher the value of breakthrough curve-shifting R&D.

---

I am principally a physical scientist, and Soheil Shayagh is principally some sort of mathematically-oriented engineer. To make a successful study, we needed to make some contact with the real world, or at least the academic literature on learning and technological innovation. To this end, we brought Dan Sanchez into the project. Dan thinks a lot about how public policy can help promote innovation and the deployment of new, cleaner energy technologies.

The result of our work was a study titled “Evaluating relative benefits of different types of R&D for clean energy technologies“, published in the journal Energy Policy. (Unfortunately, due to an oversight, our study ended up behind a paywall but you can email me at [email protected] to request a copy.)

Our results indicate that, even if steady curve-following research produces results more reliably, when successful, step-wise curve-shifting research produces much greater benefits.

Our simple calculations are highly idealized and schematic and are designed only to illustrate basic principles.

I infer from our study that, other things equal (and other things are never equal), government funded R&D should focus on trying to achieve step-wise curve-shifting breakthroughs.

I suppose my group’s research should also focus on trying to achieve step-wise breakthroughs, but that’s a tough challenge.

 

Most economists think a tax on carbon dioxide emissions is the simplest and most efficient way to get us to stop using the sky for disposal of our waste CO2. This tax could be applied when fossil fuels are extracted from the ground or imported, and credits could be given if someone could show that they permanently buried the waste CO2 underground.

This carbon tax would make fossil fuels more expensive. If the tax level continued to increase, eventually using fossil fuels (without underground CO2 disposal) would become more expensive than every other energy technology, and economics would squeeze carbon dioxide emissions our of our economy.

A tax is an anathema to most politicians. One proposal to make such a tax more palatable would be to distribute the revenue evenly on a per capita basis. Due to inequalities in income distribution, this would result in most people receiving a direct net economic benefit. This could make it politically popular. In terms of net transfer, money would be transferred from the rich and given to the poor and middle classes. Thus, a revenue-neutral carbon tax would both help eliminate carbon dioxide emissions and help reduce economic inequality. Sounds like a good thing. (Why aren’t we doing it?)

Another idea would be to institute a carbon tax to generate tax revenue that could then be used to help provide essential services such as health care, education, income subsidies, and so on. Some of the carbon tax could potentially be used to help pay down the national debt, which in the United States now stands at $165,000 per taxpayer.

Today, we have a carbon tax rate of zero and get no carbon tax revenue. When the carbon tax rate is so high that there are no longer any carbon emissions from our energy system, the carbon tax revenue will again be zero. There is some tax level in-between that would maximize revenue generation from the carbon tax. An increase in tax rate beyond this level would reduce carbon dioxide emissions so much that carbon tax revenues would start to diminish.

Whether the proceeds of the tax are distributed on a per capita basis, or used to provide essential services, people will not be happy to see tax rates rise while direct and immediate benefits from the tax decrease. These tax increases could be a tough sell for politicians. Politicians could be motivated to avoid raising the carbon tax rate, so that they can continue providing the benefits of the revenue generation to their constituents. This would result in continued CO2 emissions.

---

This issue had been nagging me for over a decade, and I have long tried to interest someone in taking the lead on addressing this question. (Avoiding work is one of my key objectives, so my usual strategy is to try to talk people into doing the work that I am trying to avoid doing myself.) Luckily, I was able to talk Rong Wang into addressing this problem. Because Rong is a physical scientist and not an economist, we were fortunate to be able to lure the economist Juan Moreno-Cruz into helping us.

Together, we produced a study titled “Will the use of a carbon tax for revenue generation produce an incentive to continue carbon emissions?“, and published it in Environmental Research Letters, where it is available for free download.

The key conclusion is represented in this figure:

Figure 1b. Projected emissions under a set of standard assumptions for three scenarios: Zero carbon tax, welfare-maximizing carbon tax, and revenue-maximizing carbon tax. Under the revenue maximizing assumption, CO2 emissions continue long into the future but at a level that is lower than would occur if there were no carbon tax at all.

Our main conclusions are: For the next decades, the incentive to generate revenue would provide motivation to increase carbon tax rates and thus achieve even lower emissions than would occur at an economically optimal ‘welfare-maximizing’ tax rate. However, by the end of this century, the incentive to generate revenue could result in too low a tax rate — a tax rate that would allow CO2 emissions to persist far into the future.

Overall, I see our result as rather encouraging. Right now, the problem is that we don’t have enough disincentives on carbon emission and politicians are having trouble motivating themselves to provide this disincentive. If revenue generation provides an additional incentive (beyond the incentive of generating climate benefits) to institute a carbon tax, that is all well and good. As mentioned above, these revenues could be distributed on a per capita basis to help combat inequality, or they could be used to provide essential services.

By the end of the century, the incentive to generate revenue could become a perverse incentive to keep carbon taxes low so that CO2 emissions might continue. However, for now, the incentive to generate revenue would motivate increased carbon tax rates, which would cause carbon emissions to decrease.

Given that today’s carbon tax rate is zero, which is clearly too low, the incentive to generate revenue can help motivate politicians to do the right thing for the climate system. That is a good thing.